Co vypadá jako romantický rozmar evoluce, je ve skutečnosti přísně řízený kalkul. Ladně svinuté spirály rozvíjející se kapradiny nebo úhledně uspořádané šupiny šišky nejsou náhoda, ale aplikovaná matematika.

Vědce proto pochopitelně zajímá, jak se ji příroda naučila. .

Leonardo Bonacci z Pisy (asi 1180-1250), který je dnes známý spíš pod jménem Fibonacci, je znám jako zřejmě nejvýznamnější matematik středověku. Namísto těžkopádného zápisu římskými číslicemi vytvořil vytvořil vlastní mnohem elegantnější způsob inspirovaný indickým a arabským systémem.

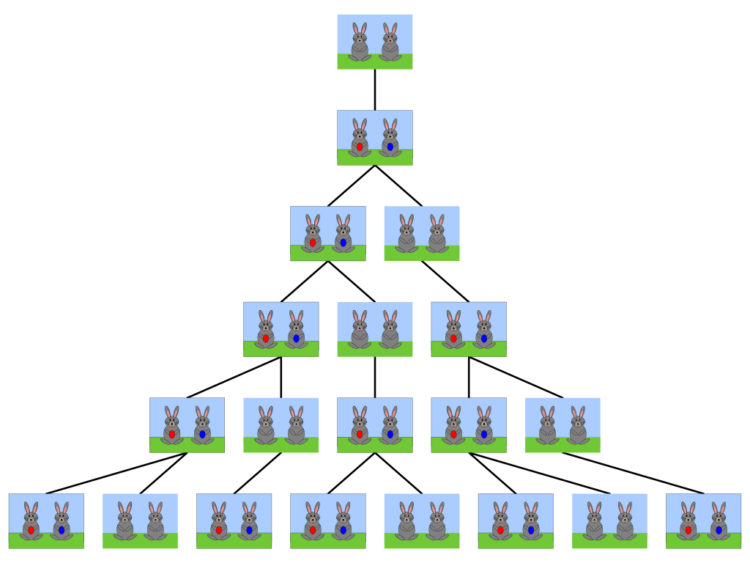
Jeho číslice zdomácněly tak, že by se na Fibonacciho jako jejich tvůrce zapomnělo, nebýt jednoho ukázkového příkladu. Šlo o výpočet, jak se mohou rozrůstat stavy králíků. Vyšel z králičího páru číslo 1. V zadání stálo, že pár je plodný od druhého měsíce a jednou měsíčně přivede na svět další pár.

Fibonacci sečetl první dva páry, rodiče a potomky, a dostal pochopitelně číslo 2. Ovšem než dospěl nový pár, byli plodní jen rodiče, a tak na další měsíc přičetl původní pár 1 a 2 nově vzniklé a měl 3 páry.

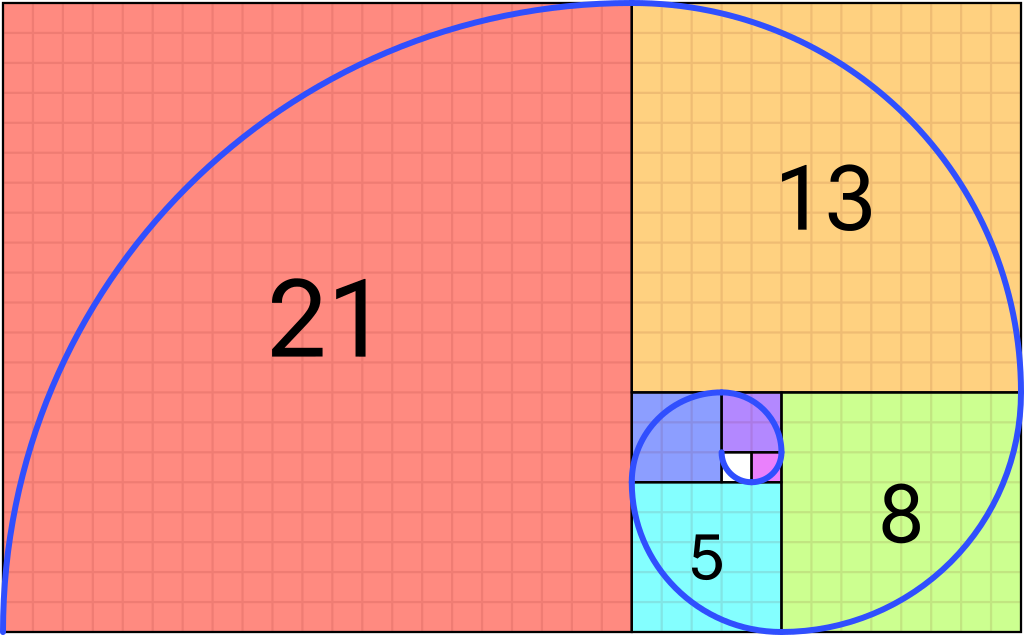
Pak už dospělo i potomstvo první generace, takže Fibonacci sečetl předchozí 2 s nově vzniklou 3 na 5. A pak už to jelo samo: 3+5=8, 5+8=13, 8+13=21, 13+21=34, 21+34=55 a tak pořád dál…

Co posloupnost umí

I když si Fibonacci zřejmě plně neuvědomil, co objevil, posloupnost nezapadla, matematici se k ní vraceli. Skutečně zajímavá totiž začne být, když se místo sčítání vydělí vyšší číslo v posloupnosti sousedním nižším.

Tedy například 34 děleno 21 nebo 55 děleno 34. Výsledek je překvapivě podobný, blíží se k 1,618. Toho si povšimly další chytré hlavy, mezi nimi Leonardo da Vinci nebo Johannes Kepler.

Když se tento řetězový zlomek převede do geometrické podoby. Vytvoří soustavu postupně narůstajících obdélníků. A teď přijde to kouzlo: Křivka spojující jejich vrcholy vykouzlí ideální poměr tvarů. Ve výtvarném umění a architektuře se mu říká zlatý řez. Rostliny ho znají také, jak si rovněž povšiml už Kepler.

I rostliny počítají

Středověk byl zlatým řezem fascinovaný. Přisuzoval mu schopnost vytvářet harmonické, ba božské proporce. Proto se jím po staletí zabývala početná pojednání o architektuře, umění a dokonce hudbě. Že může poměr 1,618 sám od sebe bez zásahu tvůrčí síly člověka fungovat i v přírodě, potvrdil šest století po Fibonaccim německý botanik Alexander Braun.

V roce 1831 začal počítat spirály, které různé orgány rostlin vytvářejí, užasl. Čísla, k nimž docházel, rozhodně nebyla nahodilá ani různorodá. Opakovala se. Hodnoty, které si zapisoval, odpovídaly číslům z posloupnosti vytvořené rodákem z Pisy.

A co bylo ještě zajímavější, počty spirál v jednom květenství nebo na jedné šišce se lišily podle toho, jakým směrem počítal. Nebyla to náhoda, ale zákonitost.

Evoluční vylepšení

K zatím nejzajímavějšímu zjištění při zkoumání Fibonacciho posloupnosti na rostlinách došel tým Holly-Anne Turnerové na Edinburské univerzitě. Tam řešili, zda je dnes převažující uspořádání podle Fibonacciho posloupnosti původním znakem nebo se vyvinulo v průběhu evoluce.

Odpověď měla dát rekonstrukce listů 407 milionů let starých fosilií kyjovitého mechu Asteroxylon mackie, považovaného za jednoho z nejstarších zástupců cévnatých rostlin. Pomocí digitálních technik a 3D tisku vytvořili trojrozměrné modely listových výhonků Asteroxylonu a zjistili, že jejich uspořádání se vzorek od vzorku lišilo.

Některé vytvářely spirály, jenže jejich počet byl buď totožný ve směru hodinových ručiček i opačném, nebo neodpovídal Fibonacciho číslům. Podle Holly-Anne Turnerové rekonstrukce mechů naznačují, že Fibonacciho posloupnost nemusela být původním vzorem pro uspořádání listů a objevila se až v průběhu času jako evoluční vylepšení.

Autorka: Kateřina Pavelcová

Více se dočtete v čísle 7/2024.